Left side figure is taken from M. Alcántara Ortigoza et al. Phys. Rev. B 74, 226401 (2006)

[Phys. Rev. B 72, 174416 (2005) and Phys. Rev. B 74, 226401 (2006)] Developing quantum computing and increasingly smaller memory storage devices has led intense research into the properties of nanoscale magnets, including quantum single-molecule magnets (SMM) and arrays of ferromagnetic nanodots. This goal, however, faces several challenges. One of them is the ever-present inter-magnet interactions, which are directly responsible for the loss of memory of these devices during magnetic relaxation. Since inter-magnet exchange interactions and some other interactions are negligibly small, it is been considered that the classical and long-range magnetic dipole-dipole interactions could be the leading factor controlling the loss of memory stored in nanomagnets’ arrays.

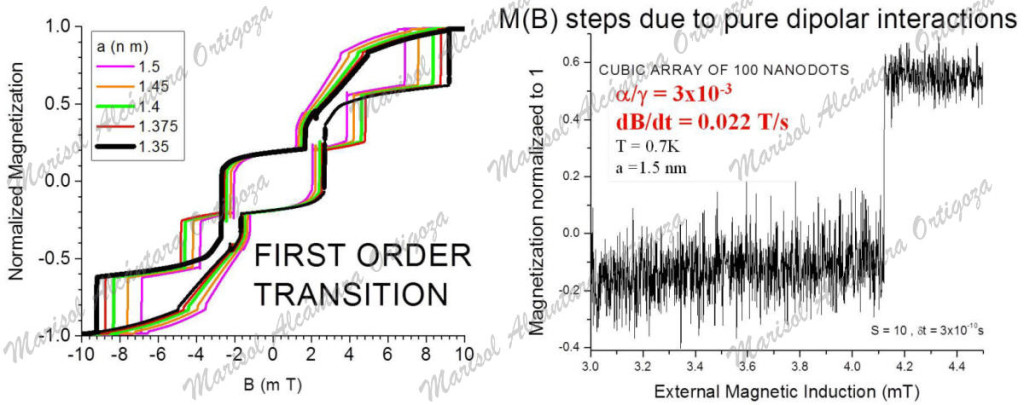
In order to gauge the importance of the dipolar interdot interaction, I have investigated the magnetization dynamics of two-dimensional squared (2D) and three-dimensional cubic (3D) arrays of ferromagnetic nanodots — subjected to their purely classical interaction [1,2]. By solving numerically the so-called Landau-Lifschitz-Gilbert equation, I have obtained the magnetic hysteresis curves and found that, even though dipolar interactions may be very weak with respect to the external magnetic induction, they suffice to demagnetize arrays of ferromagnetic dots separated by distances shorter than ~3 nm, and may thus likewise disorder SMMs. However, I have also shown that, contrary to the long known general trend, dipolar interactions may favor the magnetization of 2D arrays of dots under certain conditions.

It has been quite notable that even isolated single-molecule magnets also display magnetic hysteresis; exhibiting striking sequences of discrete steps in their magnetic hysteresis loops. A quantum tunneling picture of the magnetization mostly explains this phenomenon. Yet, there are reports of additional steps that cannot be explained by this model. In this work, in order to capture which features of SMMs are exclusive of their internal quantum nature, I have studied several factors affecting the classical magnetization/demagnetization process of the 2D and 3D arrays, including the magnetic-precession damping, dipolar interaction strength (depending on the separation between dots, i.e., dot surface or volume density), external magnetic induction rate of variation (ΔB/Δt), magnetic anisotropy of the dots, and temperature. For example, we have shown that the enlargement of magnetic hysteresis loops observed in quantum SSMs and caused by increasingly fasterΔB/Δt is also a classical effect for 3D arrays. Yet, under certain conditions, ΔB/Δt may be of negligible importance for 2D arrays, for instance. One of the most arresting results is that classical dipolar interactions also produce stepped magnetization loops for 3D arrays and hence could be the cause for the above-mentioned unexpected steps observed in SMMs. Furthermore, I have revealed that dipolar interactions can produce a first-order transition for 2D arrays, a sudden and drastic change in the magnetic hysteresis loops at a particular dot surface density. Namely, after a smooth development of the hysteresis loops, at a particular surface density (i.e., strength of dipolar interaction), the magnetic hysteresis loop changes its number of steps.  Such feature had not had not been recognized previously and had thus led to misinterpretations. Finally, I have also shown the strikingly different behavior of the magnetization hysteresis loops depending on anisotropy direction with respect to the external magnetic induction.

References 

[1] Effect of dipolar interactions on the magnetization of a cubic array of nanomagnets

[2] Comment on “Magnetization of two-dimensional square arrays of nanomagnets