Structure and free energy of Au₁₃ nanoclusters with respect to the lowest-energy isomer

[J. Phys.: Condens. Matter 24, 104026 (2012)] Phenomena at the nano-scale are subjects of wide interest because of their fundamental and technological significance. Structure characterization, stability and thermal properties of nanoparticles (NPs) are, in their own right, topics of intensive research, and today’s physicists use state-of-the-art experimental and computational techniques to unravel them. In reference [1], however, I have directed a study that shows how thoughtlessly application of certain approximations is leading to erroneous conclusions. In particular, I have called the attention to one approximation to describe the vibrational properties of a material, which was devised 100 years ago for modeling macroscopic systems and these days is unjustifiably used to describe nanoparticles.

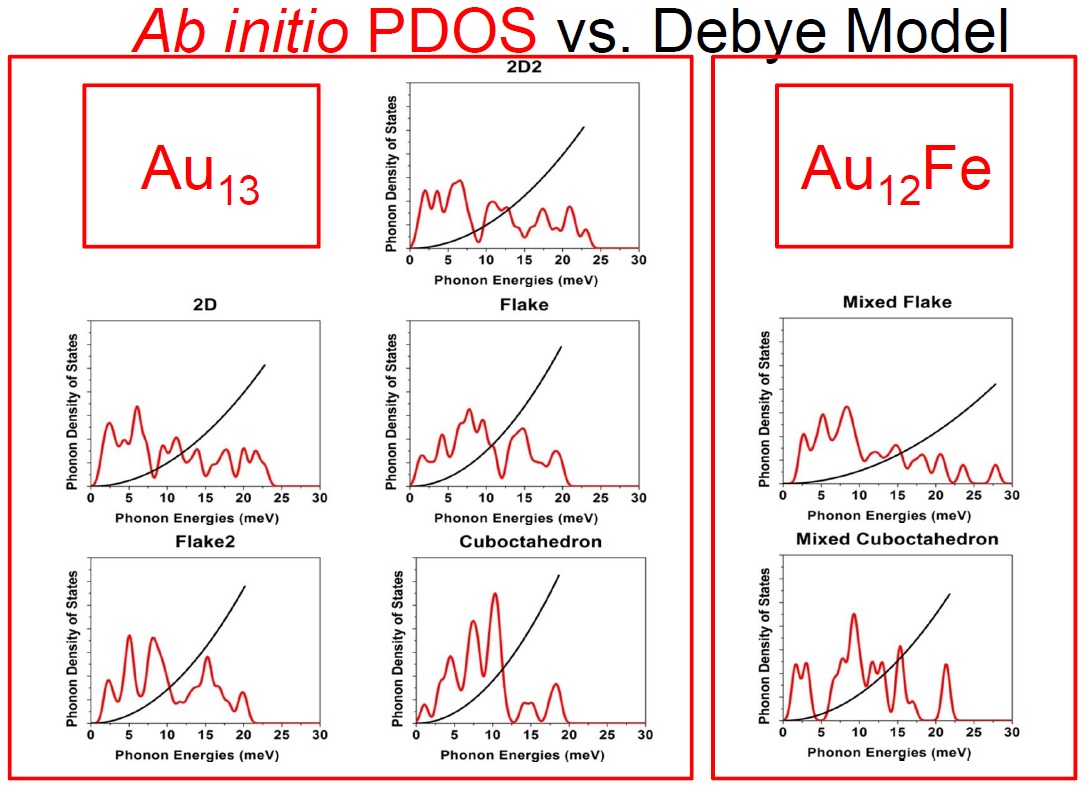
(Red) Phonon density of states of Au₁₃ isomers (PDOS) from ab initio calculations within the harmoniv approximation contrasted with the PDOS assumed within the Debye model

For example, sophisticated experiments have been performed to determine the mean-squared vibrational amplitude of small (< 2nm) nanoparticles. Based on these measurements, it was concluded that Pt atoms in some nanoparticles are held together by remarkably and unexpectedly strong bonds. Beyond the fact that such assertion cannot be right, I found imperative to demonstrate that the mean-squared vibrational amplitude cannot depict the bond strength as it does in macroscopic samples.

As experimental techniques developed for investigating the behavior of materials at lower and lower temperatures, it became evident 100 years ago that the specific heat, CV, of a material is not constant but rather at some point begins to decrease with temperature. Only with the advent of quantum mechanics and the quantization of lattice vibrations in terms of so-called phonons, it was possible to develop an expression for CV as a function of the vibrational spectrum of the material, the first great step to explain the temperature dependence of the specific heat. At that time, however, there was no experimental technique available for measuring the vibrational spectrum. Efforts thus turned to developing theoretical models that were sufficient for explaining convincingly the behavior of the specific heat at low temperatures. The most successful of these approximations was proposed by Debye, who modeled the vibrational spectrum as a continuous function of the frequency – the “Debye phonon-DOS” -, cut off at a certain frequency – the “Debye cutoff frequency”. As such, although quite successful, Debye’s model ignores altogether the discrete nature of the crystal lattice.

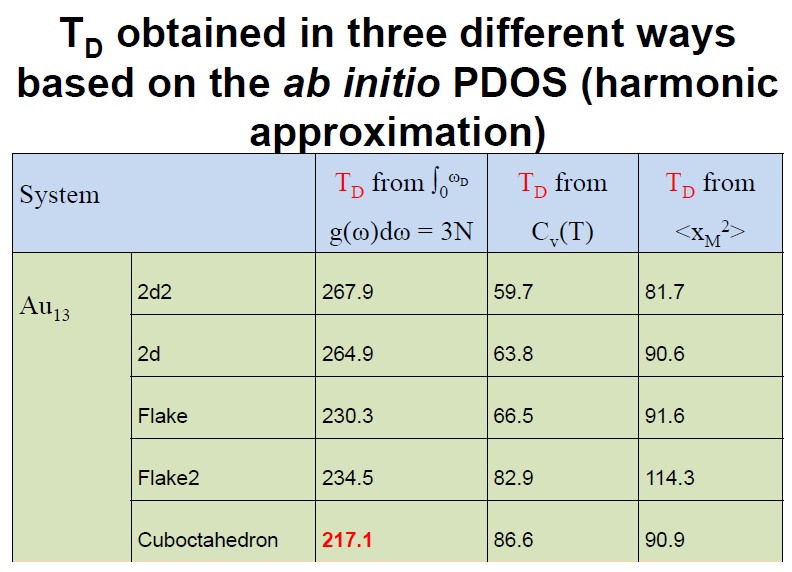The concept of the Debye temperature (TD) has been widely used in condensed matter physics to characterize numerous properties of materials. It is derived straightforwardly by associating a temperature to the Debye cutoff frequency. Thus, the Debye temperature and the Debye cutoff frequency provide equivalent information. Further, if TD of a given material is known, one can use it to estimate the velocity of sound in that material or vice versa. Also, since it also serves to model accurately the specific heat at low T with a simple formula that involves TD, if one can measure CV, then one can obtain TD and all the properties above and vice versa. Moreover, since the atom’s mean-squared vibrational amplitude (MSA) can be worked out as a function of the phonon-DOS, the Debye model is used to obtain a simple relation between TD and the MSA, which is another useful concept that enters into the interpretation of measurements.

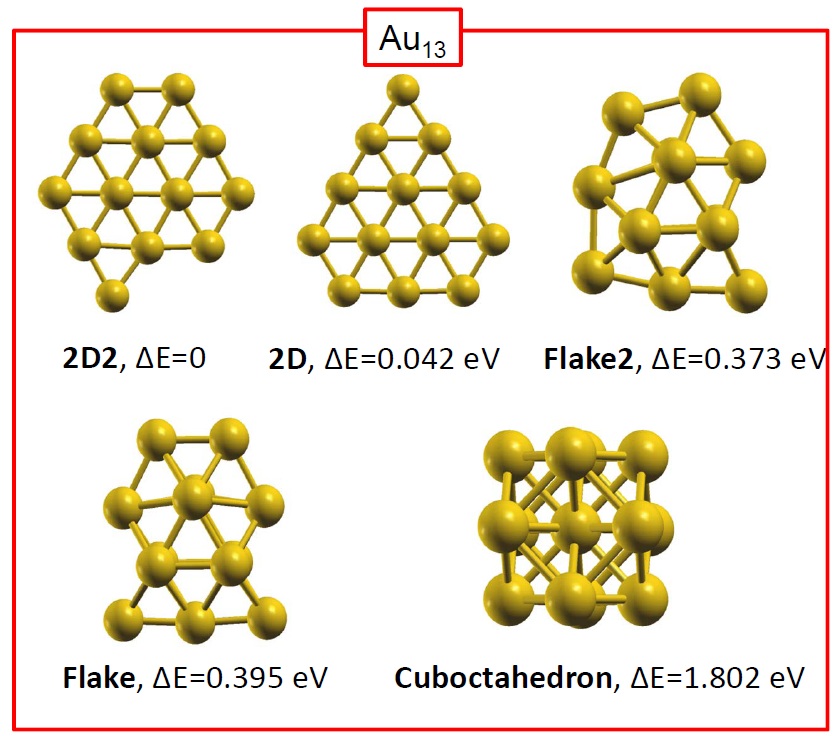
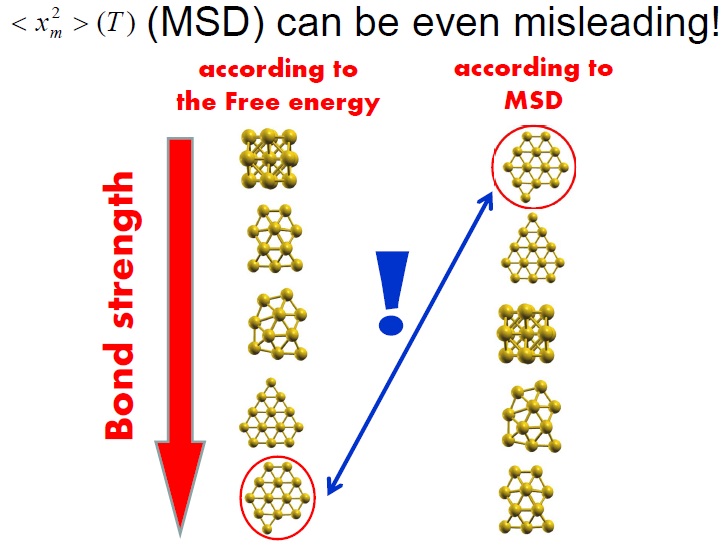In reference [1], I have used the vibrational spectrum of 13-atom nanoparticles, Au13, (with varied structures) of my coworkers to expose an extreme case, clearly showing that a continuous and monotonic model for the VDOS is, in general, simply meaningless for nanoparticles. The main reason is that at the nanoscale the discrete nature of matter cannot be neglected. To illustrate the dangers of applying the concept of the Debye temperature to nanoparticles, as it is currently done, I have derived it via three independent methods that, according to the Debye model, are equivalent: from the cutoff frequency; from the specific heat; and from the mean-square vibrational amplitude. The calculations showed that the values for ‘TD’ arrived at via these three avenues strikingly diverge. I demonstrated hence that the ‘Debye temperature’ concept is pointless for nanoparticles and, evidently, no conclusion about their properties can be drawn from it. Finally, combining total-energy calculation and the mean-squared vibrational amplitude, I have shown that the latter is no longer a quantity that characterizes the bond-strength, at least not in nanoparticles. Namely, the bond-strength characterization via the mean-squared vibrational amplitude renders totally incorrect deductions, for which experiments cannot turn to it for characterizing their relative stability, for example.

Reference:

[1] G. S. Shafai, M. Alcántara Ortigoza, and T. S. Rahman; “Is the Debye-temperature a useful concept at the nanometer scale? Insights from ab initio free energy calculations of Au₁₃ and Au₁₂Fe nanoclusters”; J. Phys.: Condens. Matter 24, 104026 (2012)