
Model structures for experimentally synthetized nanoparticles. See “Thermodynamic properties of Pt nanoparticles: Size, shape, support, and adsorbate effects”; Phys. Rev. B 84, 245438 (2011)
[Phys. Rev. B 84, 245438 (2011)] As experimentalist design better and better techniques to investigate nanoscale systems, anomalous electronic and thermodynamic properties for nanoparticles (NPs) continue being reported. Yet, despite several years of investigations, the origin of these effects was, until recently, still heavily debated.
Among the inexplicable “anomalies”, I have focused on understanding those reported for Pt NPs, which include negative thermal expansion from 100 to 700 K, low mean-squared vibrational amplitude (MSA), and low slope of the linear dependence of the MSA as a function of temperature, lower than that of Pt bulk (interpreted as “enhanced” atom-atom bond strength). Consensus exists relative to the strong influence of the size on the thermal properties of nanoscale materials, but specific causes are still ambiguous.
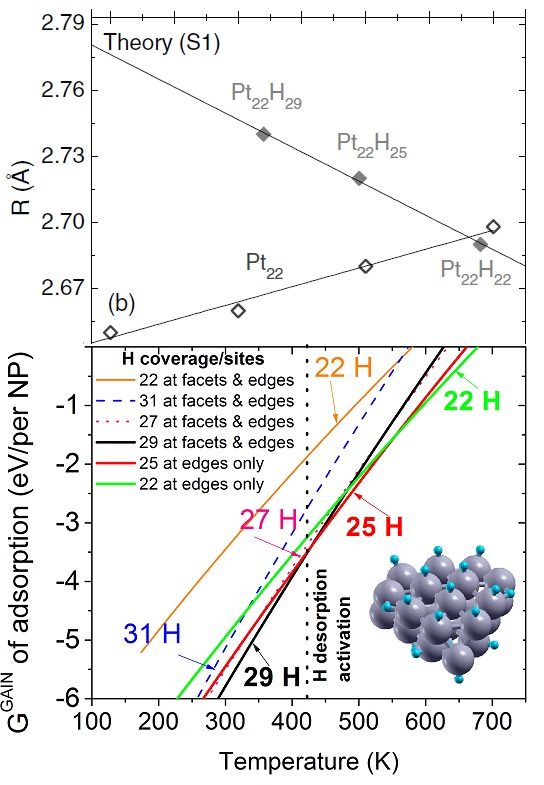
Calculated median of the Pt-Pt bond lengths of an unsupported clean Pt22 NP (open symbols, ab initio MD calculations) and an H-covered Pt22 NP plotted as a function of temperature. The solid symbols in (b) correspond to H coverages that are thermodynamically stable at the given temperature (0 K DFT calculations). The median absolute deviations range from 0.04 to 0.09 A. (c) Calculated gain in the Gibbs free energy upon H adsorption on Pt22 NP plotted as a function of temperature for varying H coverage: Pt22H22 (all H atoms on edge sites), Pt22H22 (some H atoms on facets), Pt22H25 (all H atoms on edge sites), Pt22H27, Pt22H29, and Pt22H31. The dashed line indicates the first crossover between two thermodynamically stable states. The inset in (c) shows a model Pt22H22 NP with hydrogen-covering edges and facets. The small and large circles represent H and Pt atoms, respectively. Figure taken from Phys. Rev. B 84, 245438 (2011)
In reference [1], I have directed a computational investigation to explain the negative thermal expansion of Pt NPs and the unexpectedly low slope of the mean-squared amplitude as a function of the temperature. To begin with, regardless of the origin of anomalously low MSA, I showed in a previous work (J. Phys.: Condens. Matter 24, 104026 (2012)) that this quantity does not bear information about bond-strength in the case of NPs.
The first step to conduct this investigation was to understand the experimental conditions under which the experiments in the group of Prof. Roldán Cuenya were performed: (1) The NPs were embedded in a hydrogen (H2) atmosphere, (2) the technique used to gauge the bond strength, although exchangeable with other scattering techniques (that specifically gauge the mean-squared vibrational amplitude) for studying bulk materials, actually does not exactly probe the mean-squared vibrational amplitude (MSA), and (3) the NPs were deposited on a support material.
Regarding experimental condition (1), i.e., the presence of a H2 atmosphere, I have proposed hydrogen adsorption as the cause of the apparent negative thermal expansion, based simply on a number of related experiments. In fact, calculations of my coworker, Ghazal Shafai, demonstrated that H-free Pt NPs display, as expected, a positive thermal expansion. In order to prove that the presence of H was causing the fictitious negative thermal expansion, I have combined first-principles calculations of the structure, total energy, and vibrational properties of a Pt NP for calculating the Gibbs free energy gain as a function of temperature and as a function of the amount of H on the Pt NP. My calculations showed, as I expected, that with increasing temperature the amount of H on the Pt NP that is energetically more favorable decreases and that, as the amount of H decreases, the Pt bonds shrink. With this, I demonstrated that the negative thermal expansion reported in several studies is not intrinsic but, at least in part, caused by H desorption.
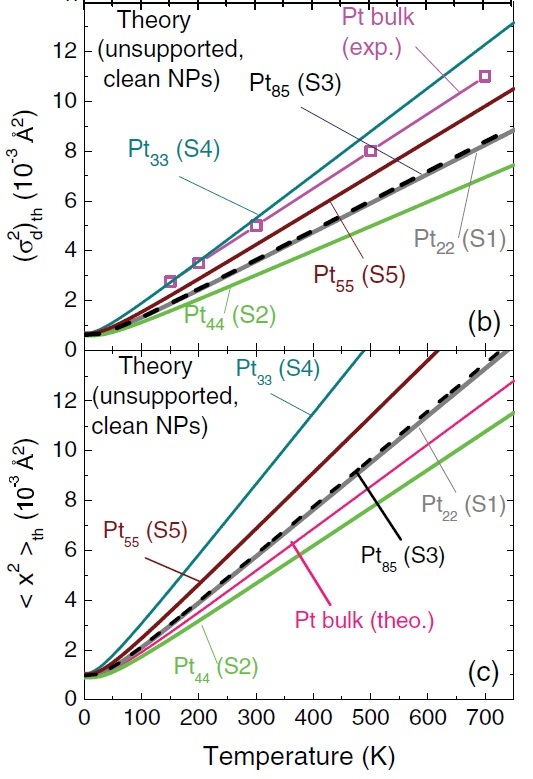
Thermal evolution of (b) the mean-squared bond-length fluctuations (MSBLF) and (c) the mean squared amplitude of the various Pt NPs. Figure taken from Phys. Rev. B 84, 245438 (2011)
Regarding experimental condition (2), i.e., the technique used to get information about the vibrational motion I have again turned to bases of the problem. It has been long recognized that the atomic mean-squared vibrational amplitude (MSA) is conceptually different from the quantity related to the atomic vibrations that is characterized by the technique (so-called EXAFS) used in those investigations reporting the “anomalous” behavior. The quantity probed by EXAFS is rather related to bond-length fluctuation parallel to the bond (MSBLF) and thus EXAFS can be understood as a technique that filters vibrational motion “components”.
Based on a still ongoing project, I pointed out that the “anomalous” slopes obtained in the experiment were not for MSA but for MSBLF and that, at the nanoscale, these two quantities are not exchangeable, not even approximately. Again, in order to prove it, in reference (1), I calculated MSA as a function of temperature via first-principles calculations of the vibrational dynamics of several NPs. I then devised a way to also calculate their MSBLF. With these two quantities in hand, I showed that the slope of MSBLF is indeed lower than the MSA of bulk Pt, just as experiments indicated. As also expected, the slope of real MSA is higher than that of bulk Pt in general. In short, if these two quantities, MSA and MSBLF, are erroneously considered “equivalent”, then of course measurements seem “anomalous”.
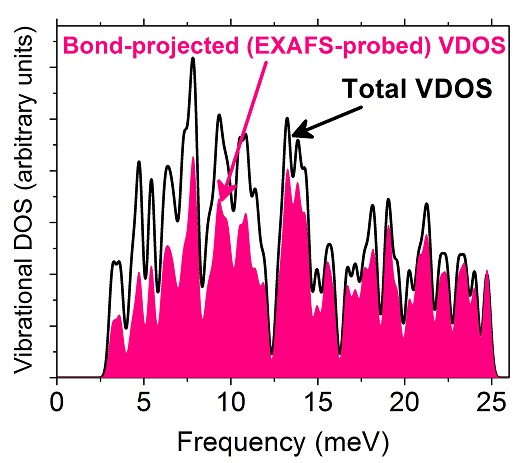
DFT-calculated total (black curve) and average bond-projected (pink/gray) VDOS of unsupported Pt85. Both are broadened by a Gaussian smearing of 0.35 meV. The pink/gray curve is representative of the lattice vibrations probed by EXAFS, which is expected to underestimate low-energy phonon modes.
Finally, regarding experimental condition (3), and again based on a still ongoing project, I have proposed in reference (1) that there are critical vibrational patterns that dominate the magnitude and slope of the MSA of a NP. These critical vibrations, however, are damped when the NP attaches to the substrate (replaced by others). This must happen for all NPs and would explain why the measured MSBLF displays smaller deviations from NP to NP than the deviation found in calculation, where the NPs are not supported. To demonstrate this effect, in reference (1) I calculated the vibrational dynamics of a gold NP supported on a ruthenium surface.
Reference:
[1] B. Roldan Cuenya, M. Alcántara Ortigoza, L. K. Ono, F. Behafarid, S. Mostafa, J. R. Croy, K. Paredis, G. Shafai, T. S. Rahman, L. Li, Z. Zhang, and J. C. Yang; “Thermodynamic properties of Pt nanoparticles: Size, shape, support, and adsorbate effects”; Phys. Rev. B 84, 245438 (2011)


