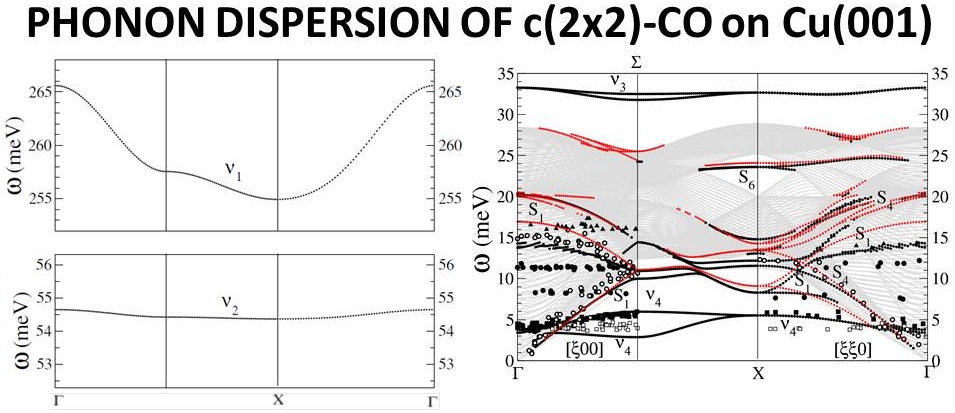
GGA-PBE phonon dispersion of c(2×2)-CO/Cu(100) taken from M. Alcántara Ortigoza et al. J. Phys.: Condens. Matter 20, 224009 (2008) and Phys. Rev. B 79, 125432 (2009). It is modelled by a Cu 50-
layer slab. Filled dots denote calculated surface modes. Experimental data correspond to Helium-atom-scattring data: Filled circles and triangles were associated with multiphonon processes. Open circles correspond to the substrate’s Rayleigh wave. Squares were associated with the FT mode of
CO on the perfect c(2×2) structure (filled) and on defects in the adlayer at lower coverage (open). The red dots are calculated surface mode of the clean surface.

[J. Phys.: Condens. Matter 20, 224009 (2008) and Phys. Rev. B 79, 125432 (2009)] Nailing down the essentials to optimally catalyze a desired reaction is still a very challenging problem. Not surprisingly, although most production processes in industry are catalyzed, most chemists and engineers are restricted to trial and error when searching for the proper catalyst.

The interest on transition (Pt, Ru, Rh, Pd, etc.) and noble (Cu, Ag, and Au) metals surface arises because of their important applications in heterogeneous catalysis. CO oxidation, for example, is a reaction that has attracted a great deal of attention in catalysis for many years now. Keeping in mind that one would like to control reactions of bigger molecules, part of the importance of this reaction is that CO oxidation is the simplest bimolecular reactions catalyzed by metal surfaces. There are however two more emphatic reasons: CO is a highly harmful exhaust from engines by far more than CO₂ and it may also block the catalysis of other desirable reactions.

Reactions on surfaces are an intricate combination of several factors: adsorption and diffusion of the reactants on the surface, metal-assisted bond breaking/creation, and desorption surface of the products. Each of these processes is a cumbersome problem in itself. Luckily, analysis of the vibrations of the system provides valuable information about the adsorption’s nature and diffusivity of the reactants. The so-called frustrated translation (FT) and frustrated rotation modes (FR) of adsorbed molecules are dynamical precursors of their diffusion on the surface and, therefore, control the diffusion rate and correlate the diffusion energy barrier. Similarly, the Metal-molecule stretch mode is a dynamical precursor of desorption and correlates the adsorption energy. The essence of the problem is that — since the adsorbates are chemisorbed — these vibrations, precursors of desired processes, can be strongly damped due to vibrational coupling and electron–hole pair creation in the metal substrate. Moreover, the lifetime of high-frequency internal vibrations may also be dramatically reduce upon chemisorption despite they lie well above all other modes in the system, as in the case of the C-O stretch mode.

Cu(001) is typically chosen to study CO diffusion because -among other reasons- it roughly allows to isolate one of the two mechanism that may hinder the diffusivity of CO on metal surfaces. The low electronic density of states of Cu at the Fermi level was expected to subdue the damping caused by electron-hole pair creation. On the other hand, since the energy of the FT mode of CO on Cu(001) was known to be very low, no overlap between Cu vibrational states and the FT was expected and therefore the excitation of Cu vibrational states was considered an insignificant damping mechanism. Yet, the lifetime of the C-O stretch mode and the FT were found to be very short despite the first one is well above the bulk band and the second one is well below the bulk band. These features have been explained by assuming multi-phonon processes relaxing the C-O stretch mode and that the potential energy surface with respect to lateral displacements of CO is not harmonic around the equilibrium position (at 0K) but quartically anharmonic. Our calculations, however, give a different perspective on these issues and on the effects of what has been considered “weak chemisorption”.

• The accepted model of atop adsorption of CO on Cu(001) and the formation of a c(2×2) overlayer has been proved to be dynamically stable.

• In the framework of the mixed basis and the pseudopotential approach, GGA (with Perdew–Burke–Ernzerhof functionals) reproduces the calculated adsorption site, adsorption energy, the Cu-C bond-length, and the C-O stretch mode, the Cu-CO stretch mode and the CO frustrated rotation at Γ. More importantly, it reproduces notably well helium atom scattering (HAS) data for the frustrated translation (FT) mode hence pointing to the harmonic nature of the Cu–CO bond at 0 K.

• CO-modes are influenced by molecule–substrate and molecule–molecule interactions:

a) The 8 meV softening of the C–O stretch mode (ν₁) caused by chemisorption is nicely reproduced by our calculation.

b) The C–O stretch mode, ν₁ (~258 meV), disperses inside the SBZ (by up to 10 meV at X), indicative of CO–CO interactions. Although inspection of the displacement vectors in our DFPT calculations confirms that the C–O stretch mode is totally independent of the dynamics of the substrate, our similar studies on CO/Ag(001) indicates that CO-CO interactions are mediated by the substrate (see link for CO on Ag).

c) Reliable calculations of the Cu-CO stretch (ν₂) and the Frustrated translation (ν₄) mode strongly depend on a proper treatment of the electronic and dynamical coupling bewteen the molecule and the substrate. Namely, accurate reproduction of ν₂ and ν₄ was possible by using GGA-PBE exchange-correlation functionals but not LDA functionals. Furthermore, omission of the dynamics of the substrate softens ν₂ by ~8 meV in DFPT calculations.

d) Examination of the real-space force constant matrices indicates that lateral interactions among CO molecules exist as well. They are at least 10 times smaller than those due to the perturbation to the C–O bond length, but enough to make the FT and the FR (to a lesser degree) modes to disperse and split their SH- and L-branches, which otherwise would be degenerate.

e) Splitting of the FT and FR branches along Σ as well as energetic considerations suggest that the lateral interaction between molecules is repulsive.

f) As expected, the low frequency of the FT avoids coupling to the substrate modes for most part of the Brillouin zone. Yet, it allows for a harmonic resonant coupling to Cu bulk modes in the vicinity of n₄over a significant region around the Brillouin zone center. The coupling is manifested through a Gaussian-like broadening of the spectral line of the FT mode even though the center of the distribution is independent of the dynamics of the substrate.

• The effects of CO adsorption on the substrate also confirm that CO chemisorption on Cu(001) is not as weak as reflected by the chemisorption energy.

a) Structural changes in the Cu surface with respect to clean Cu(001): Uneven relaxation of the CO-covered and bare atoms.

b) Changes in the DOS of covered and bare atoms with respect to those in clean Cu(001)

c) Charge redistribution induced by and on CO. Depletion of CO σ HOMO-LUMO states and of the valence charge of Cu atoms as well as population of CO anti-bonding π states and states localized around the Cu-C bond.

d) Reproduction of the measured softening of the surface Rayleigh wave. The latter shows that the softening of the surface Rayleigh wave is not due only to CO mass overloading but also due to chemisorption.

• The phonon spectrum sheds some light on the origin of the damping (linewidth) of the CO vibrational modes.

a) Although the importance of low-energy multiphonon creation in the relaxation of ν₁ is out the scope this calculation, the relatively strong dispersion found for ν₁ may account for the broadening of its linewidth and indicates that ν₁ at Γ may relax by propagation in the overlayer array (thermal conductivity) by three or four phonon processes involving ν₁ outside of the zone center.

b) HAS losses associated to triple-excitation of the FT mode are found to be surface backfolded modes.

c) Some peaks associated to double-phonon processes may correspond to a shear horizontal surface mode (backfolded S₁ along Δ) predicted to become observable upon CO chemisorption as a consequence of the symmetry of the overlayer.

d) The harmonic resonant coupling of the FT mode to Cu bulk modes, which gives rise to a Gaussian-like broadening of the spectral line of the FT mode, contravenes that the proposed quartic anharmonicity of the bond causes the unexpectedly broad line-width of this mode. At G, for example, the curve has a harmonic half-linewidth of ~0.12 meV, as predicted by extrapolating finite temperature experimental results to zero temperature.

References

[1] Effect of c(2×2)-CO overlayer on the phonons of Cu(001): A first-principles study

[2] Ab initio Calculations of the Dispersion of Surface Phonons of a c(2×2)-CO overlayer on Ag(001)